Skip to main content

1.2 遞迴應用

輾轉相除法

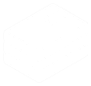
輾轉相除法在求兩數的最大公因數(GCD)，是一種非常有效率的方法，我們不需要分別找出每個質因數，就可以找到其最大公因數，以下以求330, 210兩數的最大公因數為例

步驟 圖片 解釋
1 將330,210兩數併排寫下，並用3條直線做分隔
2 用 330 除以 210，得到商為 1，餘數為 120。(重點是那個餘數)
3 用前一次的除數(210)除以前一次的餘數(120)，得到商為1，餘數為 90。
4 用前一次的除數(120)除以前一次的餘數(90)，得到商為 1，餘數為 30。
5 用前一次的除數(90)除以前一次的餘數(30)，得到商為 3，餘數為 0。當餘數為 0 時，除數30 即為 330 和 210 的最大公因數。
  • 如果以橫式來呈現除法過程會更容易看出輾轉的過程
  • 被除數=除數$\times$商+餘數
    1. $330 = 210 \times 1 + 120$
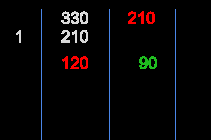
    2. $210 = 120 \times + 90$
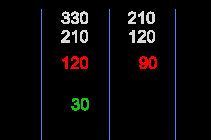
    3. $120 = 90 \times 1 + 30$
    4. $90 = 30 \times 3 + 0$
  • 可以發現以下性質
    1. 前一回合的除數是下一回合的被除數。
    2. 前一回合的餘數是下一回合的除數。
    3. 若餘數為 0，則該回合的除數即為最大公因數。
  • 最後，就可以藉由上述結果建立遞迴關係式 \[GCD(x, y)= \begin {cases} GCD(b, a \% b) & \text{if }a\% b!=0 \\ b & \text{if } a \% b == 0\end{cases}\]
  • 遞迴函數程式碼
  • Ex104輾轉相除法練習：網址

河內塔問題

問題介紹

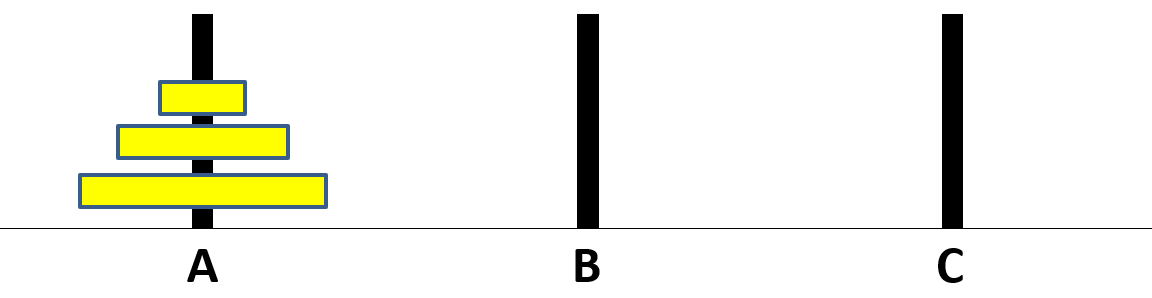
典型的三圓盤河內塔，以下為規則

  • 一次只能移動一個圓盤
  • 任何時刻，大圓盤不能在小圓盤上面
  • 所有圓盤都要從A柱移到C柱

拆解問題

  • 一個圓盤：直接將圓盤從A移到C即可

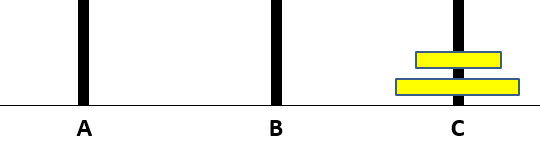
  • 兩個圓盤：在兩個圓盤中，需要將中間B柱當成緩衝區，須將最上面那一個圓盤先放置緩衝區，才可將最大的圓盤移至C柱

  • 在此，發現了一個規律，在底層圓盤移動前，上方圓盤必須先全部搬到緩衝區

  • 下一步，可建立一個函數move(discs, from, buffer, to)，discs為我們須將$1~discs$由from移到to

  • 換句話說，當$discs=1$時，代表不用在乎buffer直接將目前的盤子從from移動到to即可

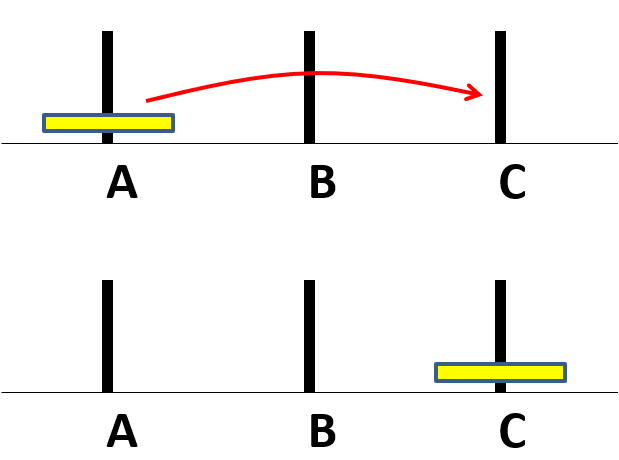
  • 當 $n=1$ 時

    • move(1, A, , C)將1由A放置C
    • 完成

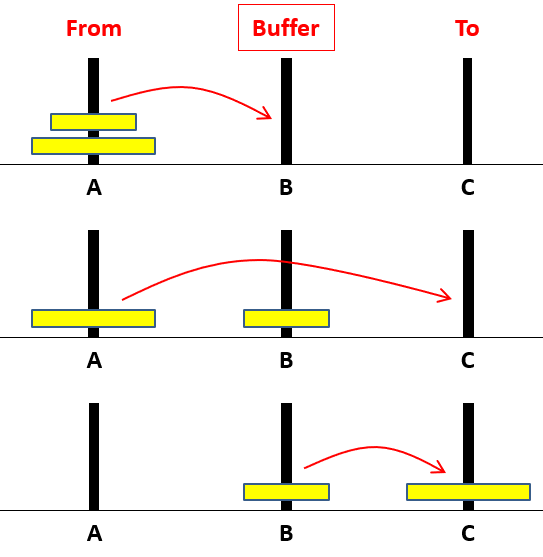
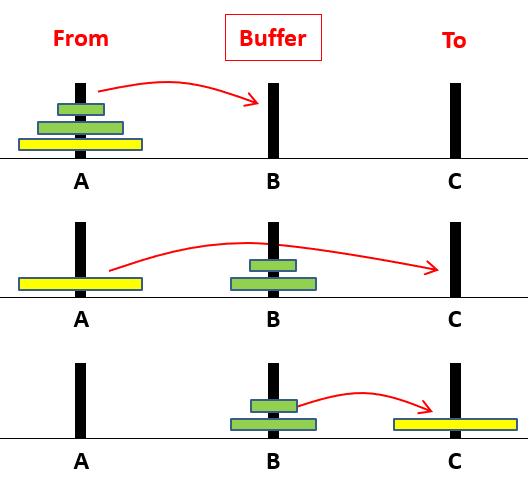
  • 當 $n=2$ 時

    • move(2, A, B, C)
      • move(1, A, , B)
      • 將在A柱中最下方圓盤移到C柱
      • move(1, B, , C)

  • 當 $n = 3$ 時(上到下編號1、2、3)

    • move(3, A, B, C)
      • move(2, A, C, B)
        • move(1, A, , C)
        • 將2號從A柱移到B柱
        • move(1, C, , B)
      • 將3號圓盤從A移至C
      • move(2, B, A, C)
        • move(1, B, , A)
        • 將2號柱從B柱移到C柱
        • move(1, A, , C)
    • 總結：若要將1~3由A移到C，要先將1~2由A移到B，接下來將3從A移到C，再將1~2由B移到C

  • Ex104河內塔：題目連結

void move(int discs, char from, char buffer, char to) 
{
  	if(discs==0)
    	return;
	move(discs-1, from , to, buffer);
    printf("move disc %d from %c to %c\n", discs, from, to);
    move(discs-1, buffer, from, to);
 }

快速冪

Back to top