Skip to main content

1.2 遞迴應用

輾轉相除法

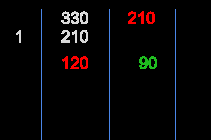
輾轉相除法在求兩數的最大公因數(GCD)，是一種非常有效率的方法，我們不需要分別找出每個質因數，就可以找到其最大公因數，以下以求330, 210兩數的最大公因數為例

步驟 圖片 解釋
1 將330,210兩數併排寫下，並用3條直線做分隔
2 用 330 除以 210，得到商為 1，餘數為 120。(重點是那個餘數)
3 用前一次的除數(210)除以前一次的餘數(120)，得到商為1，餘數為 90。
4 用前一次的除數(120)除以前一次的餘數(90)，得到商為 1，餘數為 30。
5 用前一次的除數(90)除以前一次的餘數(30)，得到商為 3，餘數為 0。當餘數為 0 時，除數30 即為 330 和 210 的最大公因數。
  • 如果以橫式來呈現除法過程會更容易看出輾轉的過程
  • 被除數=除數$\times$商+餘數 \[\begin
      {cases}
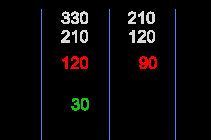
    1. $330 = 210 \times 1 + 120120$
      2. \\
    2. $210 = 120 \times + 9090$
      3. \\
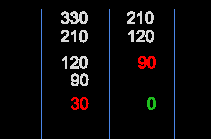
    3. $120 = 90 \times 1 + 3030$
      4. \\
    4. $90 = 30 \times 3 + 0\end{cases}\]0$
Back to top